高校数学 図形 公式 402634
中学生 高校受験情報 3 8 12年 静岡県立高校入試問題 数学 6
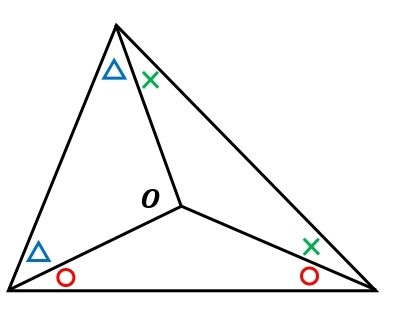
公式を覚えていても、少し構図が変わると、気付けなくなる人が多い。特に気付きにくいものを次に示した。 高校数学・受験数学の裏技関連の記事一覧 数学iaの図形問題の最終奥義:座標平面の設定 数学Ⅰ 図形と計量三角比の登場。定義をしっかり確認しましょう。 三角比の導入 数学で使う重要な三角比とその導出 三角比の相互関係とその使い方 定義からわかる三角比の有用性 (補足)三角比の相互関係の導出 三角比の拡張と単位円 \(0^\ci
高校数学 図形 公式
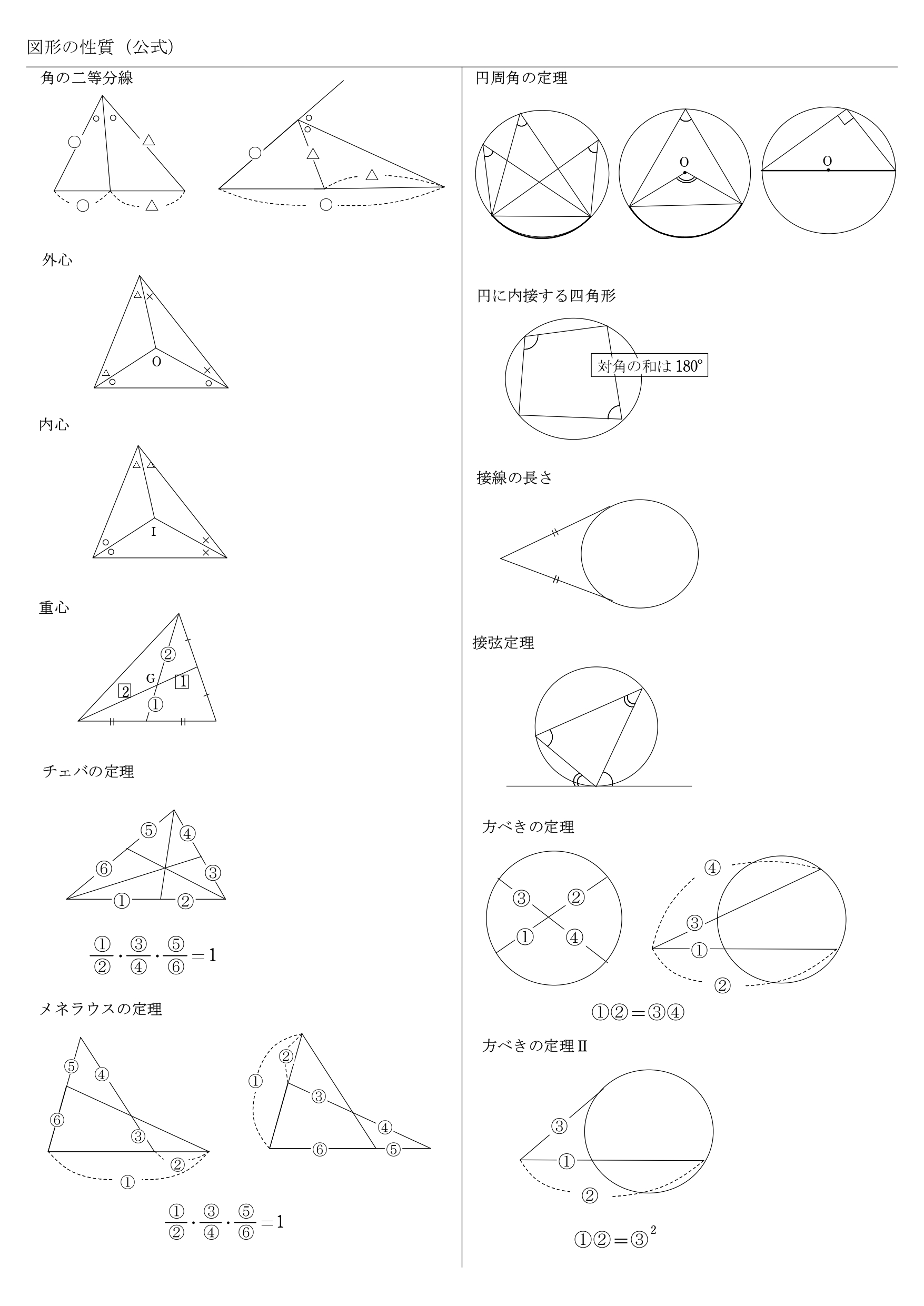
高校数学 図形 公式-高校数学の基本問題 Gogle site →数ⅠA →数ⅡB →数Ⅲ (旧C) ***最近の更新*** 集合の要素の個数(入試問題) 必要条件・十分条件(入試問題) 1次不等式(基本問題) 指数・対数,方程式・不等式(入試問題) 平面このページでは、数学Aの「図形の性質の公式」を一覧にしました。 チェバ・メネラウス・接弦定理などの公式を、わかりやすく解説しています。 問題集を解く際の参考にしてください! 目次1 図形の性
定義 定理 公式 高校数学基本事項一覧 Mathrao
各公式の右下にその公式の証明のリンクがあるので、勉強などに役立ててもらえれば幸いです。 目次 数と式 二重根号 集合と論理 集合のド・モルガンの法則 二次関数 二次方程式の解の公式 図形と計量 軸または 軸に平行な二点の間の距離は、単純に座標の引き算をすれば求めることが出来ます。 しかし、 軸にも 軸にも平行でない二点についてはそこまで簡単には求めることができません。 そのような二点の間の距離を求めるための公式は、三平方の定理 「高校数学Ⅰ三角比⑨三角不等式(2)(図形と計量#9) 000 ポイント紹介 040 (1)の解説 644 (2)の解説 1441 次回予告 # 高校数学 #三角比#三角不等式 #ココが知りたい高校数学 #ココ知り #数学Ⅰ #数学苦手 #数学解説 #大学受験数学 #定期テスト対策 #sin,cos,tan」, 学年 高
数学Ⅰ1数と式 展開公式・因数分解公式α 絶対値の性質・方程式・不等式 平方根の性質・2重根号22次方程式・2次関数 平方完成 2次方程式の解・重解・解の個数 関数の平行移動・対称移動3図形と計量 正弦定理・余弦定理 $90^{ \ 単元 立体の体積と表面積, 「75°、15°、90°の辺の比など、教科書には載っていない便利な定理・公式です。 実際に高校受験のときによく使っていました。 覚えておくとかなり役に立ちます。」, 学年 中学3年生, キーワード 三平方の定理,相似な図形,円の接線,内接円,外接円,正三角形,正ぜひ、チェックしてみてください。 高校数学A図形の性質 公式一覧(チェバ・メネラウス・接弦・方べき) このページでは、数学Aの「図形の性質の公式」を一覧にしました。 チェバ・メネラウス・接弦定理などの公式を、わかりやすく解説してい
高校数学 図形 公式のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  | |
「高校数学 図形 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「高校数学 図形 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「高校数学 図形 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「高校数学 図形 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「高校数学 図形 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「高校数学 図形 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「高校数学 図形 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「高校数学 図形 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「高校数学 図形 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「高校数学 図形 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「高校数学 図形 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |
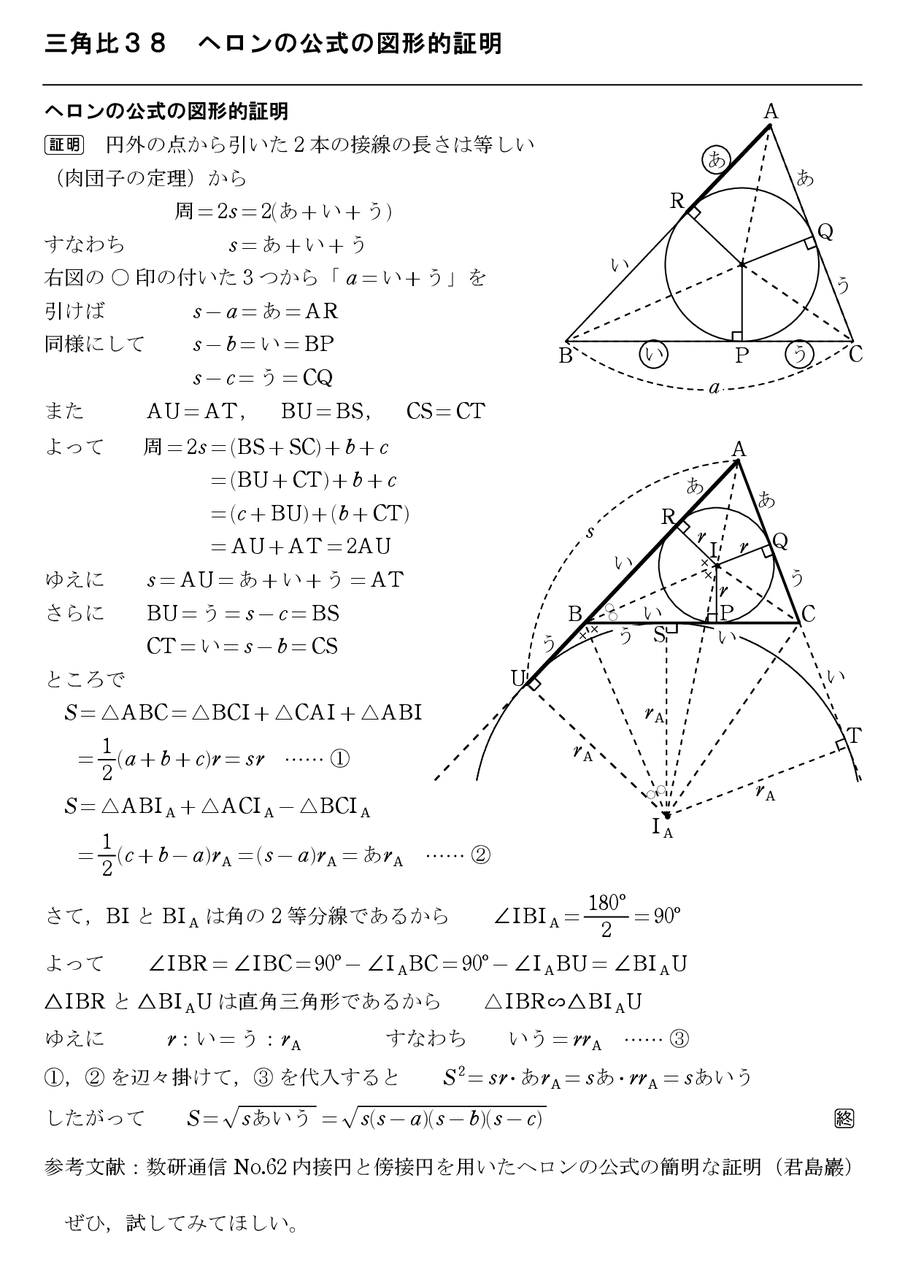
周の長さが一定である図形の中で,面積が最大のものは円です。 (等周定理) 等周定理の厳密な証明は少し大変なので,ここでは等周定理に関連して 「対称性が高い図形は面積が大きい」 というテーマで,高校数学で分かる性質をいくつか紹介します。さらに、余裕があれば、以下のヘロンの公式も知っていると良い 面積 = S s s a s b s c ( )( )( ) (sは三角形の周の半分) (5)球の体積と表面積 体積 3 3 4 = pV r , 表面積 =4pS r 2 (6)相似な図形の面積比,体積比 相似比がmnである図形の面積比は、 m n 2 2
コメント
コメントを投稿